CoderEthan学习站

深色模式

1 概念理解 ​

1.1 神经网络训练流程概述 ​

        当我们使用前馈神经网络（feedforward neural network）接收输入 x 并产生输出 y 时，信息通过网络向前流动。输入 x 提供初始信息，然后传播到每一层的隐藏单元，最终产生输出 y。这称之为前向传播（forward propagation）。 在训练过程中，前向传播可以持续向前直到它产生一个标量 的 损失函数 J(θ)J(\theta) 。 反向传播（back propagation）算法经常简称为backprop，允许来自代价函数的信息通过网络向后流动，以便计算梯度。

1.2 反向传播的定义 ​

        反向传播（英语：Backpropagation，意为误差反向传播，缩写为BP）是对多层人工神经网络进行梯度下降的算法，也就是用链式法则以网络每层的权重为变量计算损失函数的梯度，以更新权重来最小化损失函数。

2 梯度下降算法简述 ​

  • 多元函数 f 的梯度定义为：
    梯度公式

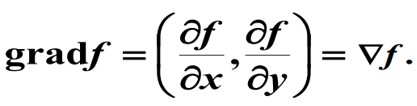
  • 梯度有一个非常重要的性质：函数f沿梯度方向增加（上升）最快, 函数f沿负梯度方向减小（下降）最快。

  • 梯度下降法(SGD)算法, ：
    梯度下降法

  • 梯度下降法效果展示：
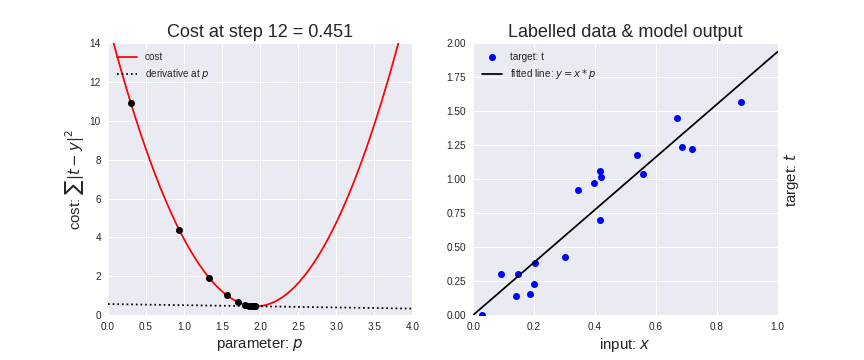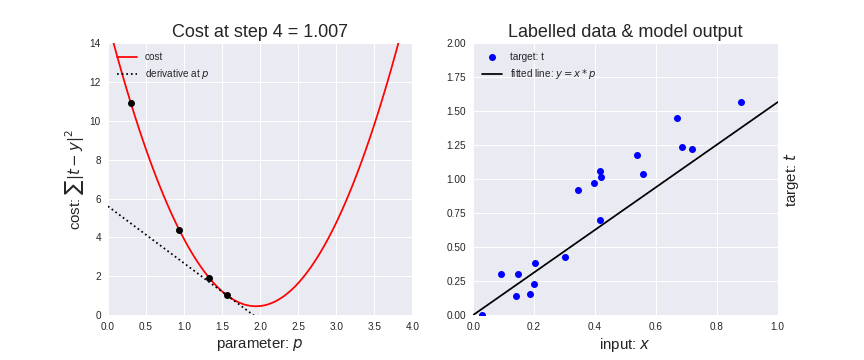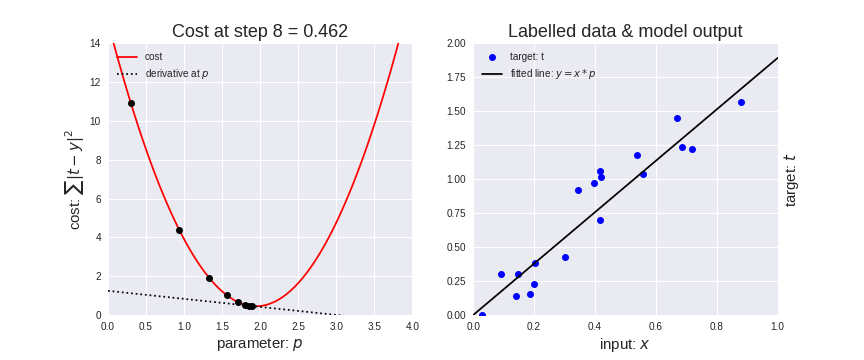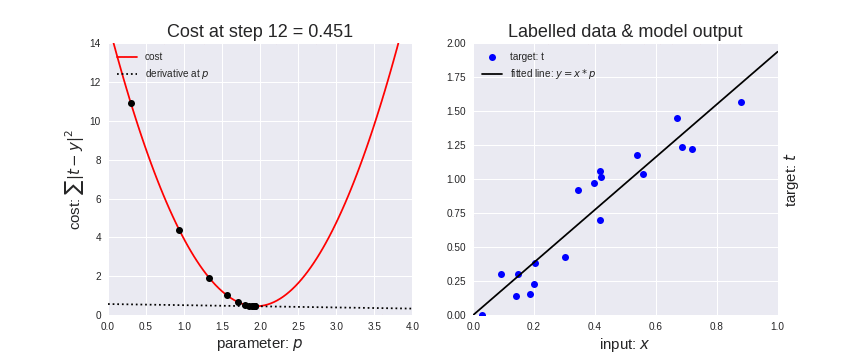
    梯度下降法

  • 梯度下降法代码展示：

python
#coding:utf8
    
def fun(x,y):
    return x*x + y*y + 2*x +2

def dfun_x(x,y): 
    return 2*x + 2 

def dfun_y(x,y):
    return 2*y

if __name__ == '__main__':    
    x = 1
    y = 4
    lr = 0.01
    iters = 4000

    for iter in range(iters):
        x = x - lr* dfun_x(x, y)
        y = y - lr* dfun_y(x, y)
        print('loss = ', fun(x, y))
        print('x=',x)
        print('y=',y)

3 BP 或 深度神经网络训练需要明确的几个概念 ​

一个典型的深度神经网络图如下：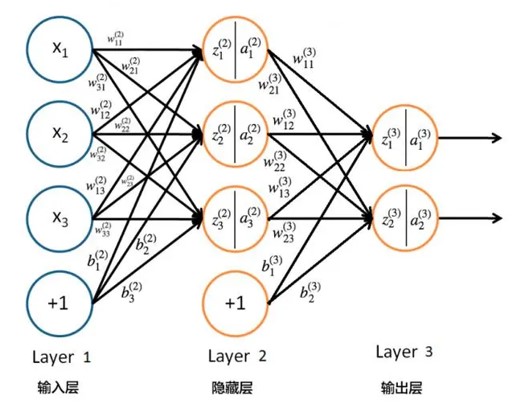
网络结构图

进一步，一个深度学习模型中的所有数据可划分为如下类别：

  • 权重(weight) 或 参数(parameter)
  • 激活(activation)
  • 超参

思考：请分析上图中参数的类别 ？？？

再进一步，按照逻辑先后顺序反向传播算法（BP 算法）可划分为两个阶段：

  • 激励传播(反向传播)
  • 权重更新

思考： 反向传播的目的是求 激活的梯度 还是 权重的梯度 ？？？
思考： 我们需要同时计算出 激活的梯度 和 权重的梯度吗 ？？？

4 链式求导法则 ​

一个深度神经网络可以理解为一个复杂的复合函数：

x=f(w);y=f(x);loss=f(y)x = f(w); y = f(x); loss = f(y)

当计算 ∂loss∂w\frac{\partial loss}{\partial w} 时就需要用到链式求导, 链式求导有两种情况需要考虑：

  • 情况一：无分支
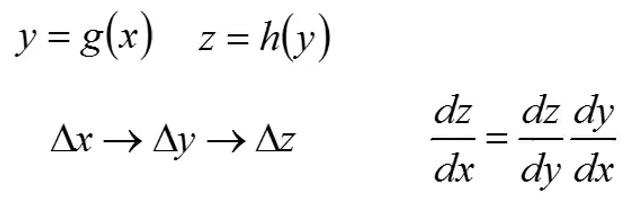
    链式求导1

  • 情况二：存在分支
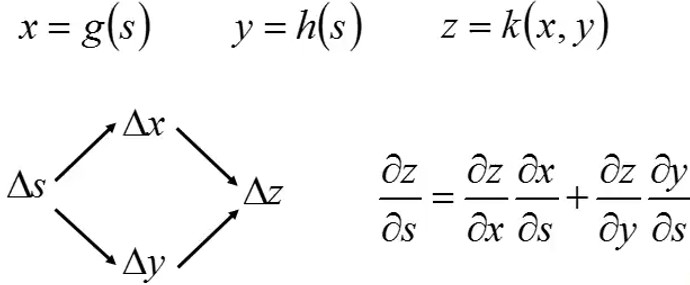
    链式求导2

===== 有了以上背景知识，我们就可以进行反向传播(back propagation) 的计算了。======

5 BP 流程图示 ​

        在前馈神经网络最后，网络的输出信号 y 与目标值(label)进行比较，这个目标值可以在训练数据集中找到。这个差异(difference)被称为输出层神经元的误差信号 δ\delta 。

error signal

        直接计算内部神经元的误差信号是不可能的，因为这些神经元的输出值是未知的。多层网络的有效训练方法长时间以来一直未知。直到上世纪八十年代中期，反向传播算法才被提出。其思想是将误差信号 d（在单个训练步骤中计算得出）传播回所有输出信号作为该神经元的输入的神经元中。

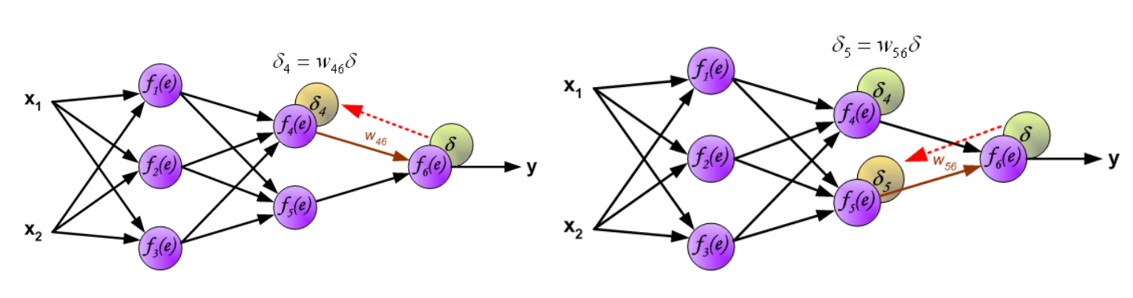
error signal propagation

        用于传播误差的权重系数 wmnw_{mn} 等于计算输出值时使用的权重系数。只是数据流的方向改变了（信号依次从输出传播到输入）。这种技术适用于所有网络层。如果传播的误差来自多个神经元，则进行相加。下面是示例图解：

error signal propagation

当计算完每个神经元的误差信号后，可以修改每个神经元输入节点的权重系数。

  • 第一层权重修改：
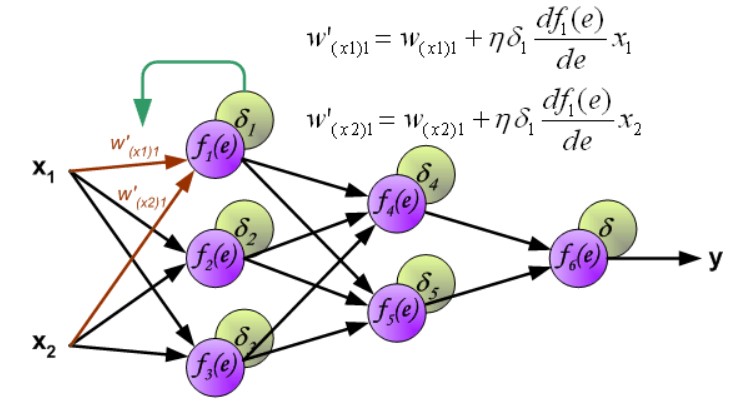
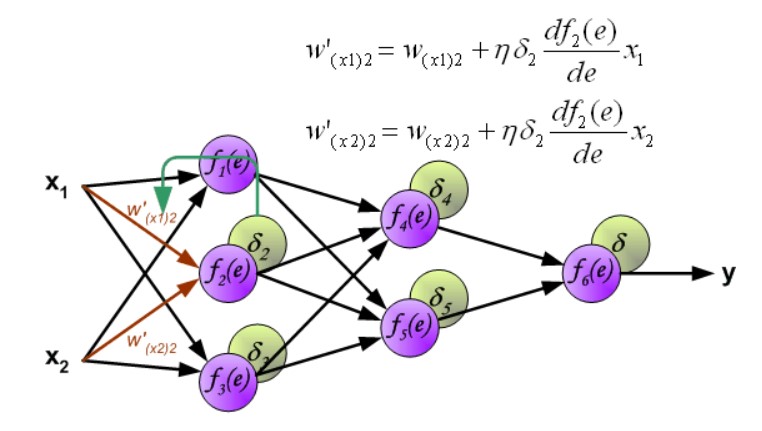
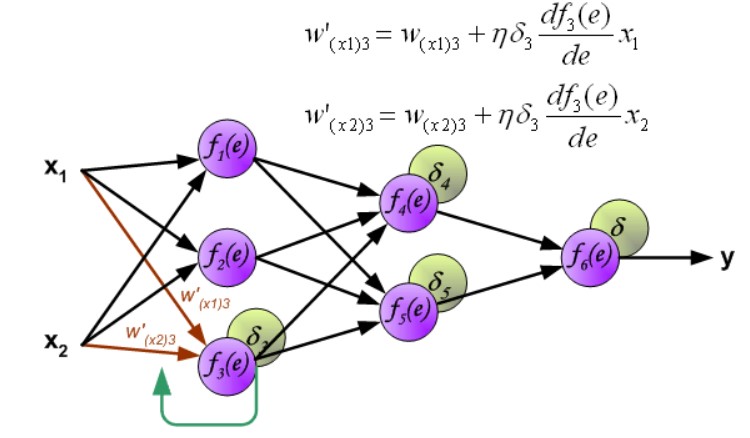
    weight updateweight updateweight update

  • 第二层权重修改：
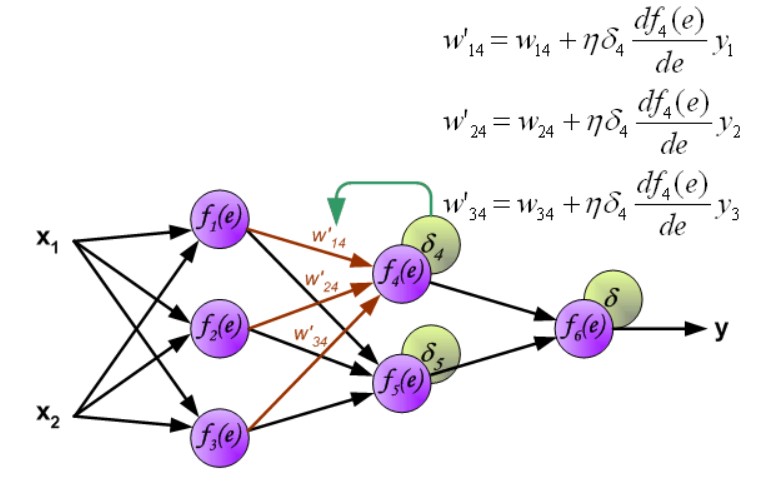
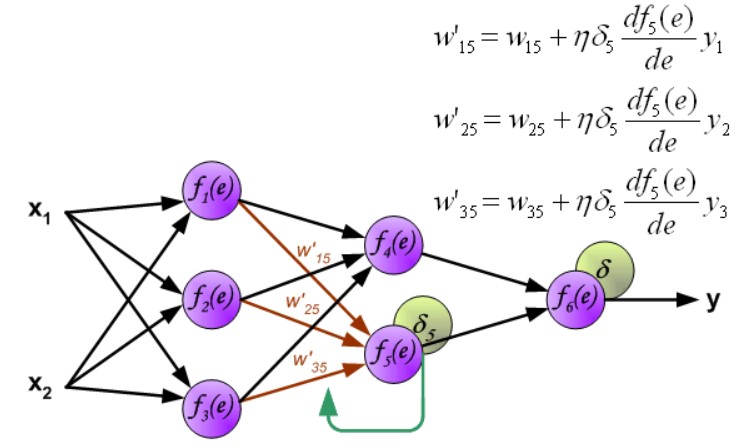
    weight updateweight update

  • 第三层权重修改：
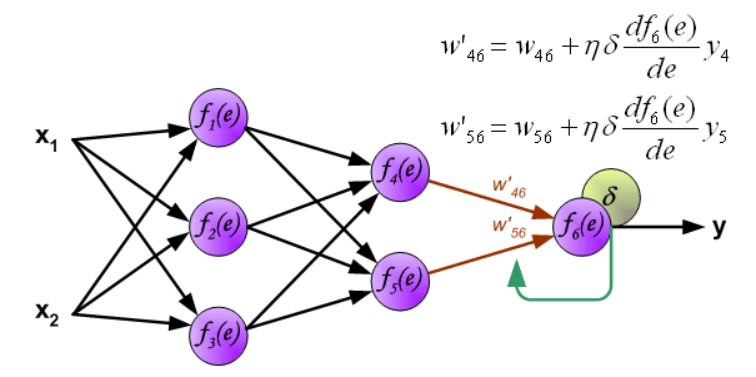
    weight update

思考：权重的梯度什么时候计算的 ？？

6 反向传播数学推导 ​

6.1 反向传播目的确认 ​

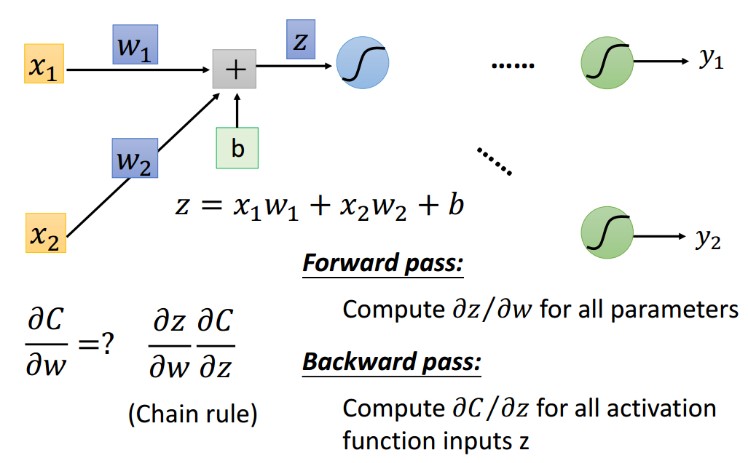
bp-target

6.2 线性连接层 weight 的梯度 ​

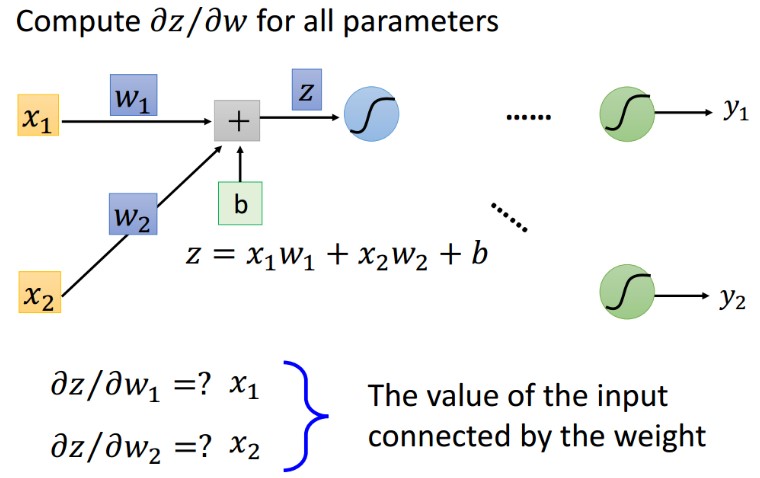
linear backward

6.3 激活函数 input 的梯度 ​

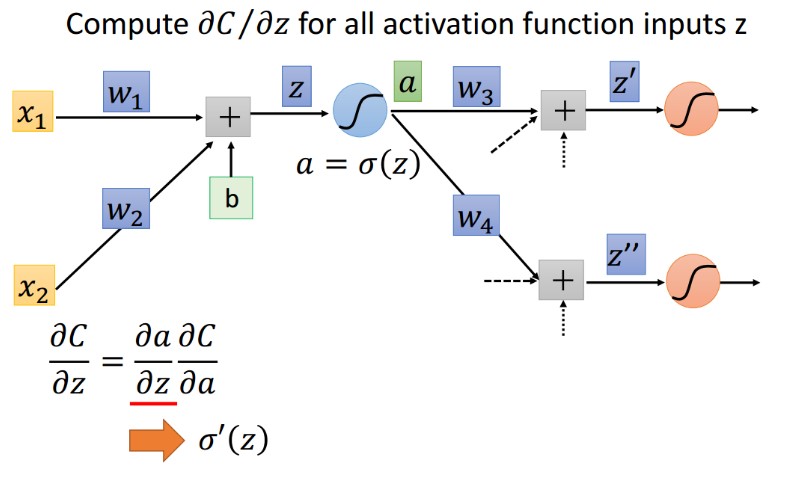
linear backward

6.4 激活函数 output 的梯度 ​

  • 求解过程
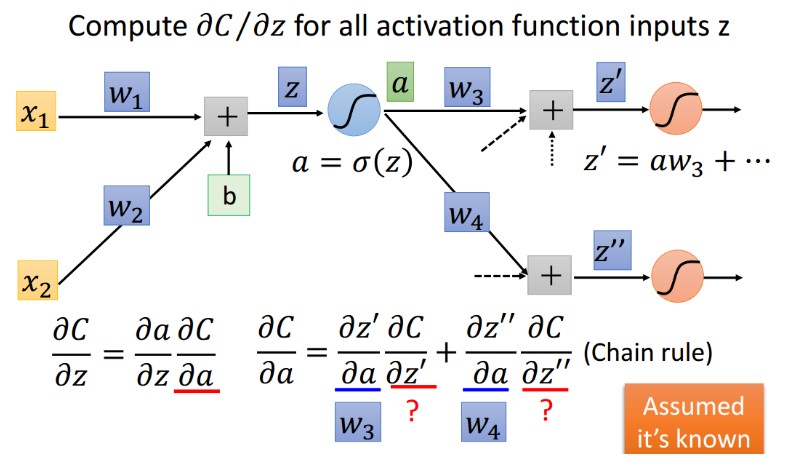
    linear backward

  • 公式化简
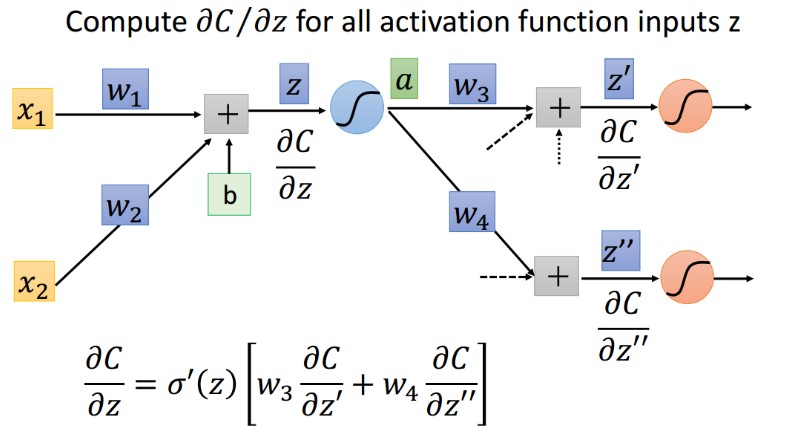
    linear backward

  • 最终形式
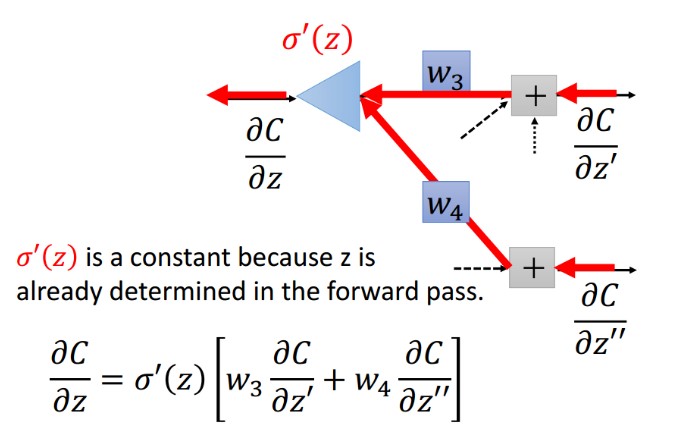
    linear backward

6.5 下层激活 input(z' and z'') 梯度求解 ​

  1. 下层是output的情况：
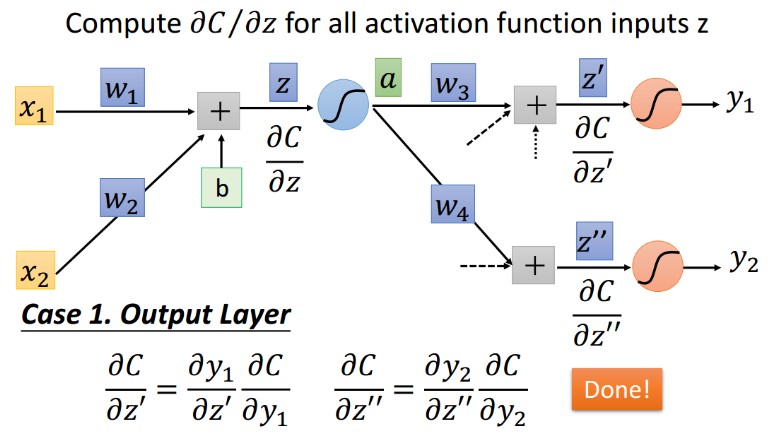
    linear backward

  2. 下层是中间层的情况：
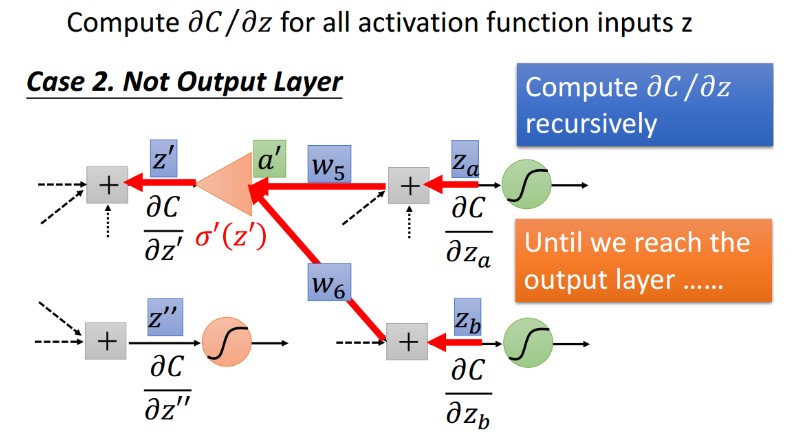
    linear backward

7 反向传播总结 ​

  • 所有激活梯度求解
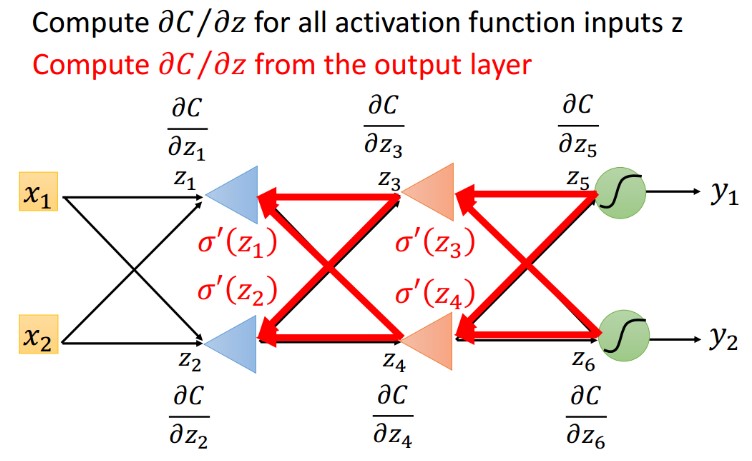
    linear backward

  • 所有权重梯度求解
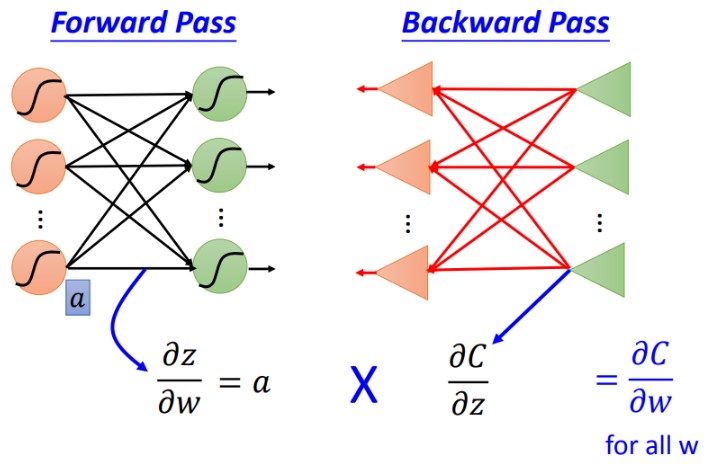
    linear backward

        损失C对W的权重有两部分，一部分是第一项，激活函数Z对W的偏导数（a）, 此项其实就是前向传播，另一个是第二项，C对激活函数Z的偏导数，此项就是反向传播。