回顾和复习整理DL

00. python基础（未补）

抽空补充

迭代器

装饰器

场景	装饰器功能	示例
训练时间统计	记录函数运行时间	`@timer`
梯度裁剪	防止梯度爆炸	`@gradient_clip(max_norm=1.0)`
模型验证模式	自动切换 `eval()` 和 `train()`	`@eval_mode`
日志记录	保存训练指标到文件	`@log_metrics(log_file="...")`
数据预处理	自动标准化/增强输入数据	`@normalize_data(mean, std)`

callable

00. 数学补充（未完全推导）

概率、几率、条件概率、联合概率等
$P(A)$ ：事情A发生的“可能性”是多少。
$Odds$ ：成功的机会与失败的机会的“比值”（或者对应概率的比值）
P(A∣B)：在已知B发生的前提下，A发生的概率。
P(A∩B)：A和B同时发生的概率。
根据上面内容引出sigmoid和softmax
熵、交叉熵、联合熵等
$H(P)$ ：一个分布有多“不可预测”？简单说就是一事件的不确定程度。熵越大，说明越“混乱”，越不确定。
$H(P,Q)$ ：用另一个分布 $Q$ 去预测真实分布 $P$ 时，我们“犯了多大错”。
联合熵：两个变量一起的“不确定性”。
KL距离和KL散度
KL散度衡量“两个概率分布差了多少”。
极大似然估计
极大似然估计是一种“反推”模型参数的办法，它认为你观察到的数据就是最有可能的现实，然后去找那个最可能解释现实的参数。（有点类似最小二乘）
- 1.似然函数：在某个特定参数下，我们观测到的数据有多“可能”出现。
- 2.取对数
- 3.对2作为目标函数，求极大值（或者负对数的极小值）
- 4.参数解析式的求法：a.直接求解（有对数，不方便），b.采用梯度下降思想
- 5.参数确定后，上游任务确定

01. Activation🌟🌟🌟

1. 我的记录：

为啥需要Activation？（深度学习往往只说非线性Attention）
都是Linear（或者Covn）的话网络还是线性的，多层和一层没啥太大区别。
有哪些类型？（工程上主要类别）
一种是point wise的操作（或者叫做element wise操作），也就是逐元素操作；另一种是具有相关性操作
Note: 公式、图像、导数图像、优缺点……
A类：数据间独立
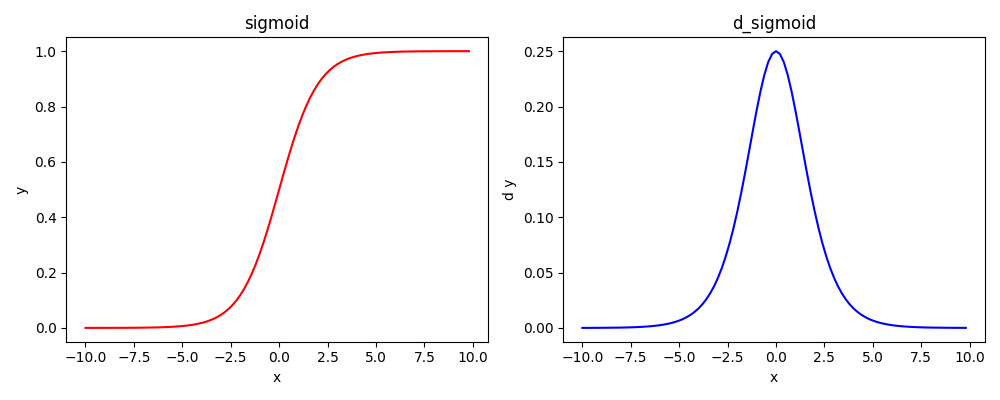
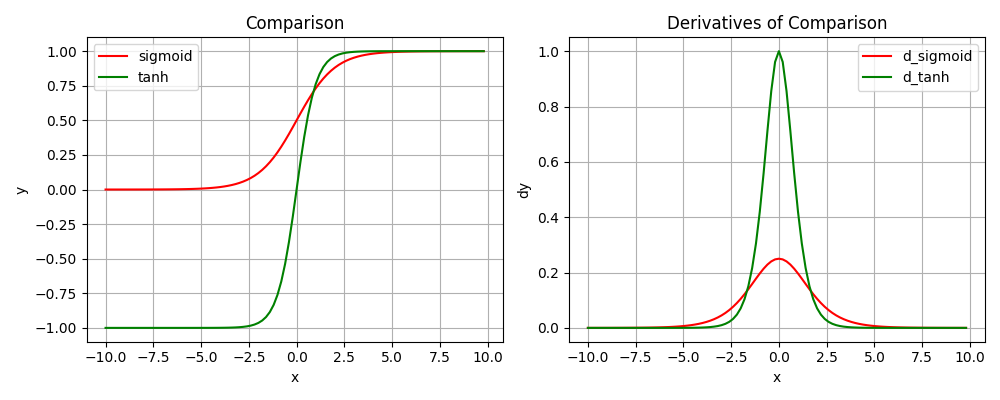
1. S型：
  - sigmoid（0.5的二分类问题）
    梯度链式法则累乘会趋近于0，两层的最值也就是0.25，多层可想而知
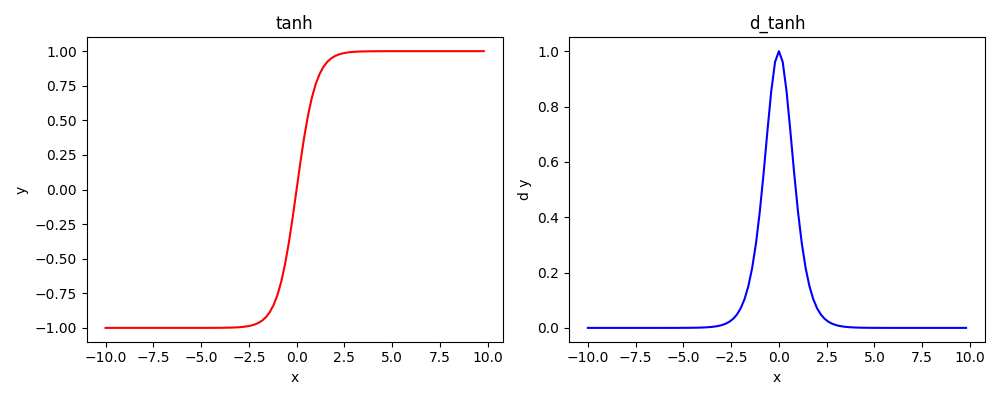
  - Tanh（NLP的递归系列常用）
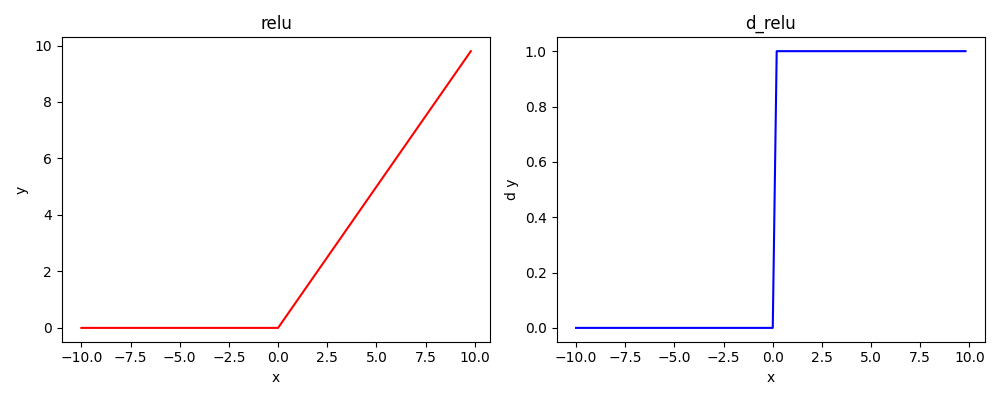
2. ==ReLU==：AlexNet里面提出。
  - ReLU
    但是神经元或者链路太少，会有0的导数，更新不易
  - 缓解激活值指数性增长=>ReLU6
  - 缓解神经元坏死现象=>Leakey ReLU=>PReLU/RReLU
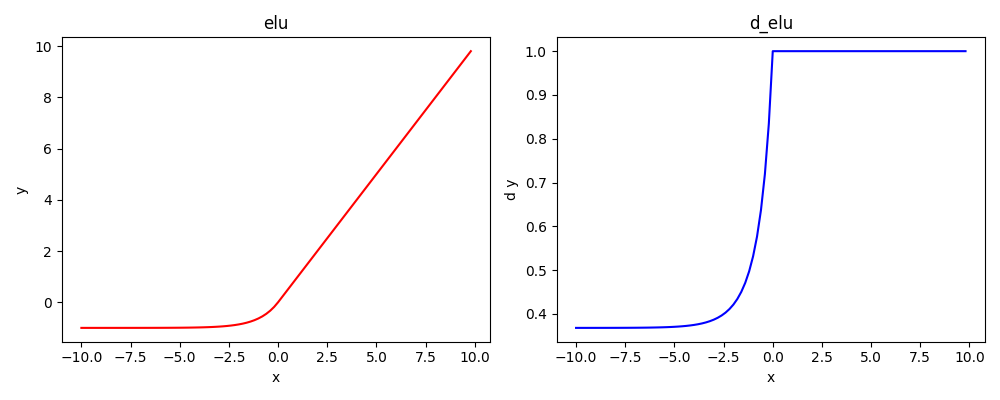
  - x=0处平滑过渡=>ELU/SELU
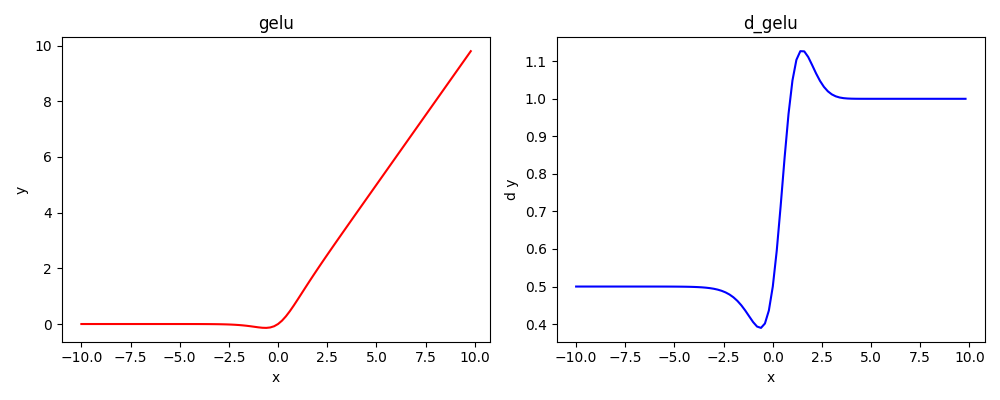
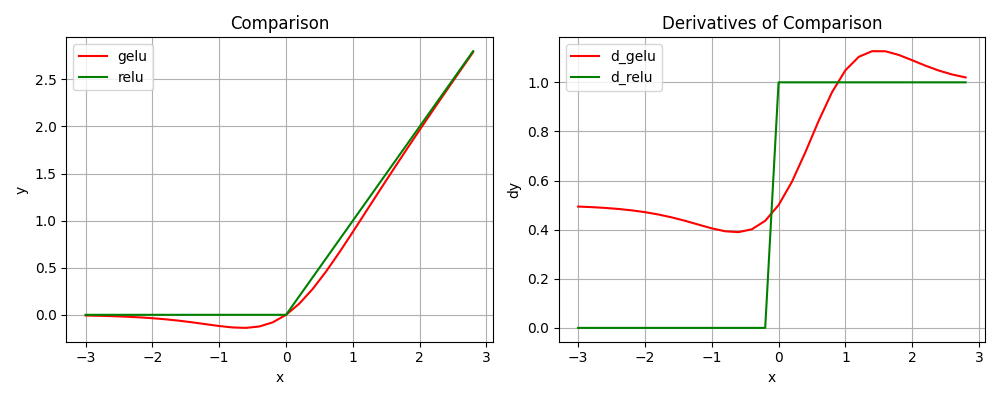
  - ==GeLU==（工程上有点简化，现在大模型都会用他的变种）
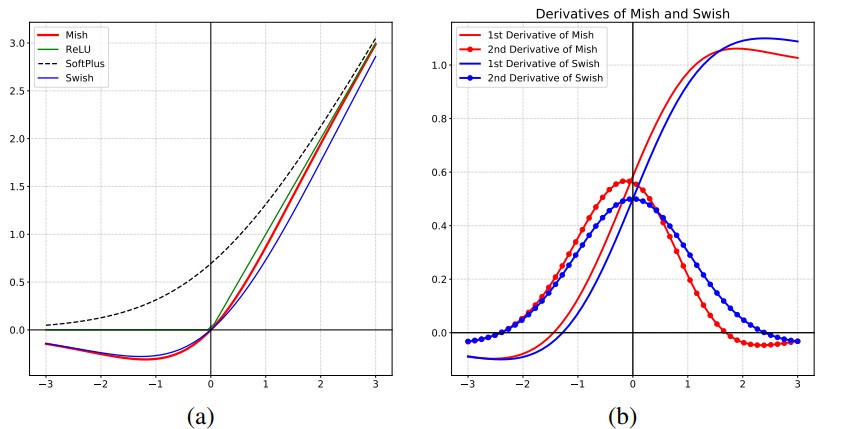
3. Swish：
  - Switch（对sigmoid进行修改）
  - Hard Swish（对ReLU6做修改，计算更简单）。“凑图像”
4. mish：平滑性更高（看一阶和二阶导图像）
B类：数据间有相互作用
1. ==softmax==；想想sigmoid。这个是多分类，单调非负归一
  类似操作还有矩阵乘法等
$sigmoid = \frac{1}{1 + e^{-x}}$
\frac{d(sigmoid)}{dx} = sigmoid(x) · (1 - sigmoid(x))
$Tanh = \frac{e^x - e^{-x}}{e^x + e^{-x}}$
$\frac{dTanh}{dx} = 1 - Tanh^2$
$ReLU = max(0, x)$
$\frac{d(ReLU)}{dx} = \left\{\begin{matrix} 1, x > 0 \\ 0, x <= 0 \end{matrix}\right.$
$ReLU6 = \left\{\begin{matrix} x,\ \ 0 <= x <= 6 \\ \ \ 6,\ \ x < 0 \ or \ x >6 \end{matrix}\right.$

Leakey \ ReLU = \left\{\begin{matrix} x,\ \ x >= 0 \\ ax,\ \ x < 0 \end{matrix}\right. \ a为常数 PReLU = \left\{\begin{matrix} x,\ \ x >= 0 \\ ax,\ \ x < 0 \end{matrix}\right. \ a为训练参数 RReLU =\left\{\begin{matrix} x,\ \ x >= 0 \\ ax,\ \ x < 0 \end{matrix}\right. \ a为随机数 ELU = \left\{\begin{matrix} &x,&x >= 0 \\ &a(e^x-1),&x < 0 \end{matrix}\right. \ a为超参数 SELU =\lambda ·\left\{\begin{matrix} &x,&x >= 0 \\ &a(e^x-1),&x < 0 \end{matrix}\right. \ \lambda和a为超参数

超参数a=1时

GELU(x)=xP(X≤x)\\ \ \ \ \ \ \ \ \ =xΦ(x) xΦ(x)≈xσ(1.702x) xΦ(x)≈\frac{1}{2} ×[1+tanh(\sqrt{\frac{π}{2}}(x+0.044715x^3))]

Swish = x·Sigmoid(\beta x) Hard\ Swish = x·\frac{ReLU6(x + 3)}{6}

$\text{Softmax}(x_{i}) = \frac{e^{x_i}}{\sum_je^{x_j}}$

$\frac{\partial y_i}{\partial x_j} = \begin{cases} y_i (1 - y_i), & \text{if } i = j \\ - y_i y_j, & \text{if } i \ne j \end{cases}$

$J = \begin{bmatrix} y_1(1 - y_1) & -y_1 y_2 & \cdots & -y_1 y_n \\ -y_2 y_1 & y_2(1 - y_2) & \cdots & -y_2 y_n \\ \vdots & \vdots & \ddots & \vdots \\ -y_n y_1 & -y_n y_2 & \cdots & y_n(1 - y_n) \end{bmatrix}$

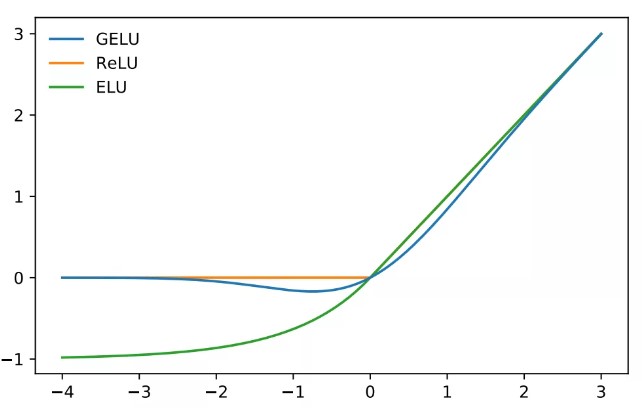
源码里面有所优化：

$\text{Softmax}(x_{i}) = \frac{e^{x_i - max(x)}}{\sum_je^{x_j - max(x)}}$

💡 实际意义：

Softmax 的导数不是独立的，每个输出值的梯度都跟其它的有关。

2. 简单总结（未优化）：

激活函数	数学表达式	优点	缺点	适用场景
Sigmoid	$\frac{1}{1 + e^{-x}}$	输出在 (0,1)，适合概率输出	梯度消失、非零均值、计算较慢	二分类输出层
Softmax	$\frac{e^{x_i}}{\sum_j e^{x_j}}$	多分类概率分布，输出总和为 1	对极端值敏感，计算成本高	多分类输出层
Tanh	$\frac{e^x - e^{-x}}{e^x + e^{-x}}$	输出在 (-1,1)，零均值	梯度消失问题	RNN、数据对称场景
ReLU	$\max(0, x)$	计算高效，缓解梯度消失	神经元死亡（负值输出为 0）	CNN、默认隐藏层激活
Leaky ReLU	$\begin{cases} x & \text{if } x \geq 0 \\ \alpha x & \text{if } x < 0 \end{cases}$	缓解神经元死亡问题	需手动调参（如 α=0.01）	深层网络替代 ReLU
PReLU	Leaky ReLU，但α可学习	自适应斜率，更灵活	增加参数量	复杂任务、深层网络
ELU	$\begin{cases} x & \text{if } x \geq 0 \\ \alpha(e^x - 1) & \text{if } x < 0 \end{cases}$	平滑负值，缓解梯度消失	计算复杂（含指数运算）	需要处理负值的场景
GELU	$x \cdot \Phi(x)$ Φ 为标准正态 CDF	平滑柔和，适合深度网络	计算复杂	Transformer、BERT 等模型
Swish	$x \cdot \sigma(\beta x)$ （β可调）	非单调，实验性能优于 ReLU	计算较复杂	EfficientNet 等先进网络
Mish	$x \cdot \tanh(\ln(1 + e^x))$	平滑、无上界，缓解梯度消失	计算成本高	计算机视觉任务
Step	$\begin{cases} 1 & \text{if } x \geq 0 \\ 0 & \text{if } x < 0 \end{cases}$	二元输出	不可微，无法用于梯度下降	早期感知机（现已少用）

3. 我的思考：

对于类似softmax这种同一条数据的分母相同的，每次是否需要重新计算分母？（底层是否会做cache？）
PyTorch源码里面的Softmax激活提及了NLLLoss，这是什么？与交叉熵又是什么关系？
softmax的导数推导。
softmax输入的shape和梯度的shape不一样大吗？参数更新的时候又是怎样子的？

02. 常用Torch算子

torch.nn

1. Convolution（未补）

2. 线性变换层

Linear/Gemm

Note: Linear的weight是转置存放的

python

self.weight = Parameter(
            torch.empty((out_features, in_features), **factory_kwargs)
        )

Matmul
type与Linear的不同
要满足广播机制

3. Normlization🌟🌟🌟🌟

类型Batch Norm，Layer Norm，Instance Norm，Group Norm，RMS Norm

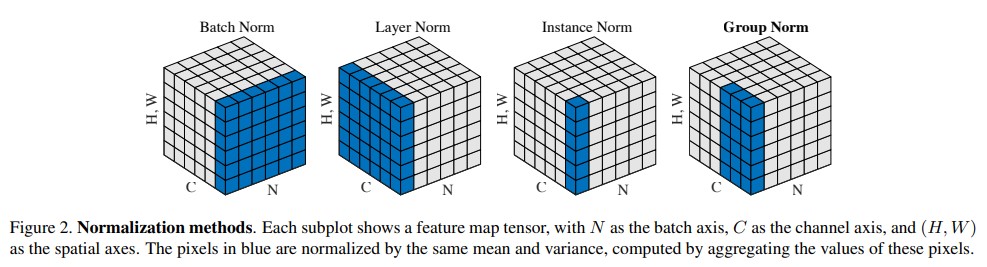
公式
$y = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta$
功能
- 去量纲，把数据调整到更强烈的数据分布
- 减少梯度消失和梯度爆炸
- 主要是有一个计算期望和方差的过程
- 做Norm的粒度不同，应用场景不同
- 其他资料：Batch Norm的技术博客
特征和不同
- 粒度不同（维度不同），对应应用领域不同
Batch Norm是逐channel（每个batch的同一个channel）进行标准化，也就是垮batch的。图片恰好需要这种方式。
LN是逐batch进行标准化的。NLP中往往是一个一个的seq进行训练的，而且长度不同，更适合这种。这让我想起了Attention的soft max操作是对一个行向量进行归一化的
LayerNorm有助于稳定训练过程并提高收敛性。它的工作原理是对输入的各个特征进行归一化，确保激活的均值和方差一致。**普遍认为这种归一化有助于缓解与内部协变量偏移相关的问题，使模型能够更有效地学习并降低对初始权重的敏感性。**从架构图上看，LayerNorm在每个Transformer 块中应用两次，一次在自注意力机制之后，一次在FFN层之后，但是在实际工作中不一定如此。
文本长度不确定，而在LN层可以。
应用场景确定LN
BN期望和方差计算策略
训练时：一个batch内计算
推理时：采用移动指数平均，不依赖于batch。会有历史信息在，有点类似RNN了
- $E_n = \alpha E + (1- \alpha)E_{n-1}$
- Var 同理
阶段使用的统计量是否更新 running_mean/var 是否依赖 batch 数据
训练当前 batch 的 μ, σ² ✅ 更新 ✅ 依赖
推理训练累积的 running_mean/var ❌ 不更新 ❌ 不依赖

阶段	使用的统计量	是否更新 running_mean/var	是否依赖 batch 数据
训练	当前 batch 的 μ, σ²	✅ 更新	✅ 依赖
推理	训练累积的 running_mean/var	❌ 不更新	❌ 不依赖

在训练和推理时有何不同？

pytorch的模型有两种模式，在module模块里面有个training属性，也有对应的API，里面明确指出了这个
在BatchNorm采用训练时计算的结果（E和Var），应用到测试或者推理的时候
在Dropout后续会说，训练会drop掉，但推理不会，会改成（1-rate）

python

def train(self: T, mode: bool = True) -> T:
    r"""Set the module in training mode.

    This has any effect only on certain modules. See documentations of
    particular modules for details of their behaviors in training/evaluation
    mode, if they are affected, e.g. :class:`Dropout`, :class:`BatchNorm`,
    etc.

    Args:
        mode (bool): whether to set training mode (``True``) or evaluation
                     mode (``False``). Default: ``True``.

官方文档说明：

BachNorm1d

RMS Norm(大模型使用)🌟🌟🌟
来源于LN，简化了LN
减均值相当于平移，这里直接去掉平移，只保留缩放
把乘法直接放进来了，

对LN做简化，对于NLP，对缩放敏感，对平移不敏感，所以分子不减 $E_x$ ，减少了很大计算量

补充部分：

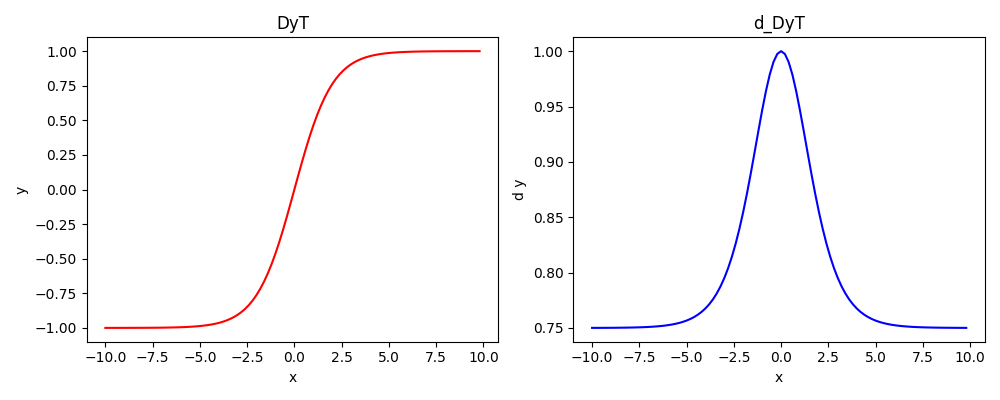
DyT(Transformers without normlization)
Transformers without normlization
$Norm:\ \gamma * \frac{(_x - E_{_x})}{\sqrt (Var_{_x})} + \beta$
$DyT:\ \gamma * Tanh(\alpha * x) + \beta$
Pre-Norm（大模型使用）和Post-Norm
结合Transformer那块知识，一个是在残差前，一个在残差后
Output_{post}=LayerNorm(x+SubLayer(x)) \\ Output_{pre}=x+SubLayer(LayerNorm(x))

公式1:PostNorm(x)=x+LayerNorm(FeedForward(x+LayerNorm(Attention(x)))) \\\\ 公式2:PreNorm(x)=x+FeedForward(LayerNorm(x))+Attention(LayerNorm(x))

特性	Post-Norm	Pre-Norm
公式	公式1	公式2
位置	残差后	残差前
出现时间	原始 Transformer（Vaswani et al., 2017）	之后发展（如 GPT-2 等）
优点	收敛后表现略好（某些任务）	更稳定，训练深层模型不易梯度消失
缺点	深层模型中容易梯度消失/爆炸	可能最终性能略低，但更容易训练
应用情况	BERT、初版Transformer	GPT系列、T5、LLama等大模型

模型	归一化类型
DeepSeek	Pre-Norm
GPT-2/3/4	Pre-Norm
BERT	Post-Norm
T5	Pre-Norm
LLaMA	Pre-Norm
Transformer XL	Pre-Norm
原始 Transformer	Post-Norm

DeepNorm
DeepNorm 是微软在 2022 年提出的改进方法（论文 "DeepNet: Scaling Transformers to 1,000 Layers"），基于 Post-Norm 但大幅提升了深层训练的稳定性，可支持超深层（如 1000 层）Transformer 的训练。
原始残差结构:
$x_{l+1} = LayerNorm(x_l + F(x_l))$
DeepNorm:
$x_{l+1} = \text{LN}(\alpha \cdot x_l + G_l(x_l, \theta_l))$

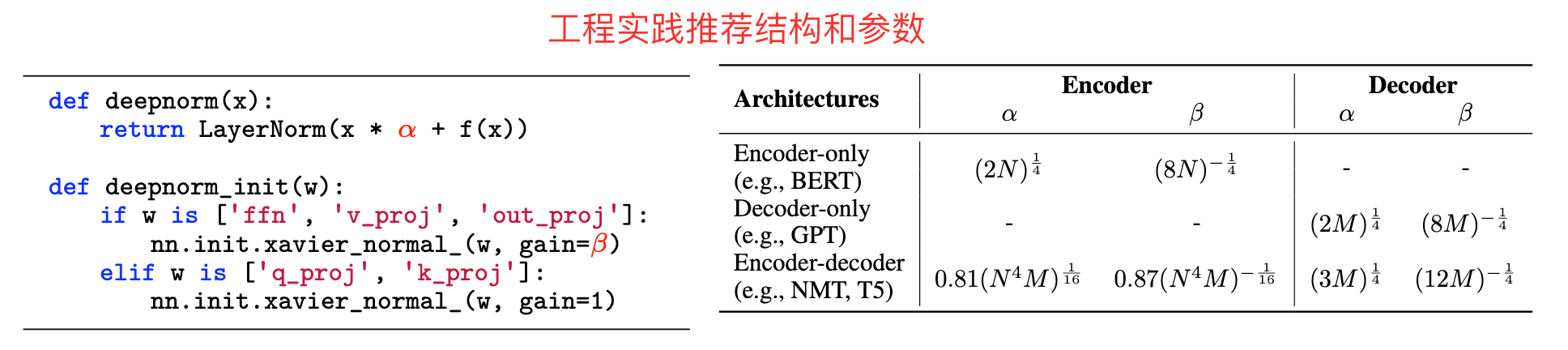
**思考：**DeepNorm中的 $\beta$ 是哪里的参数？

Note：整体回顾一下算子部分，引入后面的算子，不然大脑还停留在norm部分

4. Polling(CV)

作用

增大感受野
减少特征图尺寸，保留重要信息，降低计算量
降采样，减少噪音
位置变化鲁棒性增强

其他

对应有个out position矩阵

类型

Max、Avg等

5. activations（看01部分）

这里面内容较多，直接看01章节

[01. 激活函数🌟🌟🌟](#01. 激活函数🌟🌟🌟)

6. 其他

7. 特别的一些Operator🌟

reshape、view、permute、transpose

可能需要补充一下PyTorch的Tensor知识
比如：matedata和storage；data、storage、data_ptr、stride、contiguous；state、state_dict等

reshape
返回具有与输入相同数据和元素数量的张量，但具有指定的形状。
原始数据内存排布不变，只变shape
view
The returned tensor shares the same data and must have the same number
类似reshape，原始数据不变
要求张量是连续的**（contiguous），否则会报错（可先调用 .contiguous() 解决）。**
permute
返回原始张量输入的视图，其维度进行了排列。
permute会对数据底层重排，支持多个轴进行交换
transpose
返回一个张量，它是输入的转置版本。
类似permute，会对数据重排，支持两轴交换

Tips:

view()：当tensor连续时tensor.view()不改变存储区的真实数据，只改变元数据（Metadata）中的信息, 调用view方法张量必须连续的。
reshape()：当tensor连续时和view()相同，不连续时等价于contiguous().view()
permute()：通过改变张量的步长（stride）重新排列张量的维度，但会导致张量在内存中的存储变得不连续
contiguous()：开辟新的存储区，确保张量在内存中是连续存储，在permute()操作后需要接contiguous()才能接view()
stride()：在指定维度（dim）上，存储区中的数据元素，从一个元素跳到下一个元素所必须的步长
pytorch的存储方式：metadata+storage
metadata保存：size,dimension,stride等元信息
storage保存：以一维数组保存对应的张量数据

操作	用途	是否共享内存	连续性要求	灵活性
`view`	改变形状	是	必须连续	需元素数量一致
`reshape`	改变形状（自动处理连续性）	可能否	无	同 `view`
`transpose`	交换两个维度	是	可能破坏连续性	仅交换两个维度
`permute`	重新排列所有维度	是	可能破坏连续性	可任意调整顺序

squeeze、unsqueeze

是对维度的压缩和扩充
增加一个维度，减少一个维度

concat、stack、expand、flatten

concat
与split相反操作，可以指定某轴
stack
支持新增一个轴进行拼接
expand
支持广播机制
flatten
拉平成一维

pointwize类型

……

split、slice reduce类型

8. Embedding（可能需要单独一节）

结合Tokenizer

对分词器分到的结果进行Embedding
有一个Embedding表，直接根据index查到
计算原理：传入weight大小，把Embedding table里面的提取

9. Dropout🌟🌟🌟

功能
原理
丢弃 => 置零
随机性，不然会神经元坏死
训练和推理有啥不同
推理直接去掉，把连接weight乘以（1-p）

10 . 我的思考：

不同的Norm的参数量
可学习参数和均值方差
不同Norm操作维度，Conv操作维度，Polling操作维度
方法可训练参数量关键区别
Batch Norm 2C2C 对通道归一化，依赖 Batch 统计
Layer Norm 2D2D 对样本归一化，含 γ,βγ,β
RMS Norm DD 仅保留 γγ，无 ββ
其他哪些算子的底层是copy还是in-place
如何实现训练和推理不同的情况？（相当于加锁或者if else）

方法	可训练参数量	关键区别
Batch Norm	2C2C	对通道归一化，依赖 Batch 统计
Layer Norm	2D2D	对样本归一化，含 γ,βγ,β
RMS Norm	DD	仅保留 γγ，无 ββ

03. BP神经网络&BaseLine

1. 什么是深度学习

应用场景（多看看招聘网站和公司官网）
回顾机器学习（构造特征属性到目标标签的映射关系）
由人的经验去判断的，大部分都可以用模型实现

2. BP神经网络

3. BaseLine

思考：

矩阵实现？矩阵乘法求梯度？

04. Loss Function

入手损失函数之前，我们需要回温一下整个模型训练流程，大方向要有（或者说为啥要损失函数、作用是啥）
补充一下数学相关内容（在大方向上讲，然后入细节）

1. 类型

PyTorch官网

绝对误差

\ell(x, y) = L = \{l_1,\dots,l_N\}^\top, \quad l_n = \left| x_n - y_n \right|

平方误差

\ell(x, y) = L = \{l_1,\dots,l_N\}^\top, \quad l_n = \left( x_n - y_n \right)^2

结合MAE和MSE

$\ell(x, y) = L = \{l_1, ..., l_N\}^T$

$l_n = \begin{cases} 0.5 (x_n - y_n)^2, & \text{if } |x_n - y_n| < delta \\ delta * (|x_n - y_n| - 0.5 * delta), & \text{otherwise } \end{cases}$

交叉熵

\ell(x, y) = L = \{l_1,\dots,l_N\}^\top, \quad l_n = - w_{y_n} \log \frac{\exp(x_{n,y_n})}{\sum_{c=1}^C \exp(x_{n,c})} \cdot \mathbb{1}\{y_n \not= \text{ignore\_index}\}

负对数似然（不同分布）
逻辑回归（或者softmax回归）的损失函数
KL散度
$L(y_{\text{pred}},\ y_{\text{true}}) = y_{\text{true}} \cdot \log \frac{y_{\text{true}}}{y_{\text{pred}}} = y_{\text{true}} \cdot (\log y_{\text{true}} - \log y_{\text{pred}})$
等等等

2. 正则化

数学基础：拉格朗日函数、KK T条件等

L1
lasso 回归
L2
ridge 回归

3. 应用场景

回归任务：

损失函数	公式	应用场景
均方误差 (MSE)	\frac{1}{n}∑(y_i−\hat y_i)^2	默认选择，对异常值敏感（因为平方放大误差），要求数据高斯分布。
平均绝对误差 (MAE)	\frac{1}{n}∑∥y_i− \hat y_i∥	稀疏异常值场景。
Huber Loss	分段	平衡MSE和MAE，对异常值鲁棒且光滑，需手动设定阈值δ。

分类任务：

损失函数	公式/特点	应用场景
交叉熵损失 (Cross-Entropy)	$-\sum y_i \log(\hat{y}_i)$ （二分类/多分类）	分类任务默认选择，对错误预测惩罚高（梯度随误差增大）。
二元交叉熵 (BCE)	$-\sum [y_i \log(\hat{y}_i) + (1-y_i)\log(1-\hat{y}_i)]$	二分类任务（如垃圾邮件检测）。
Focal Loss	$-\sum \alpha_t (1-\hat{y}_i)^\gamma \log(\hat{y}_i)$	类别不平衡场景（如目标检测），通过γ降低易分类样本的权重。
Hinge Loss	$\sum \max(0, 1 - y_i \hat{y}_i)$	支持向量机（SVM），最大化分类间隔。
KL散度	$ y_{\text{true}} \cdot \log \frac{y_{\text{true}}}{y_{\text{pred}}} = y_{\text{true}} \cdot (\log y_{\text{true}} - \log y_{\text{pred}})$	概率分布匹配（如生成模型、迁移学习）。

05. Tokenization

所处的位置（哪一步需要分词）
Tokenizer

1. 类型

词粒度
字粒度
Subword粒度
Unigram Language Model
WordPiece
字节对编码（BPE）
BBPE（DeepSeek等）

2.问题

BPE如何保证推理时不出现OOV呢？

06. Optim

所处位置，作用。

回顾和复习整理DL ​

00. python基础（未补） ​

00. 数学补充（未完全推导） ​

01. Activation🌟🌟🌟 ​

1. 我的记录： ​

2. 简单总结（未优化）： ​

3. 我的思考： ​

02. 常用Torch算子 ​

1. Convolution（未补） ​

2. 线性变换层 ​

3. Normlization🌟🌟🌟🌟 ​

4. Polling(CV) ​

5. activations（看01部分） ​

6. 其他 ​

7. 特别的一些Operator🌟 ​

8. Embedding（可能需要单独一节） ​

9. Dropout🌟🌟🌟 ​

10 . 我的思考： ​

03. BP神经网络&BaseLine ​

1. 什么是深度学习 ​

2. BP神经网络 ​

3. BaseLine ​

04. Loss Function ​

1. 类型 ​

2. 正则化 ​

3. 应用场景 ​

05. Tokenization ​

1. 类型 ​

2.问题 ​

06. Optim ​

回顾和复习整理DL

00. python基础（未补）

00. 数学补充（未完全推导）

01. Activation🌟🌟🌟

1. 我的记录：

2. 简单总结（未优化）：

3. 我的思考：

02. 常用Torch算子

1. Convolution（未补）

2. 线性变换层

3. Normlization🌟🌟🌟🌟

4. Polling(CV)

5. activations（看01部分）

6. 其他

7. 特别的一些Operator🌟

8. Embedding（可能需要单独一节）

9. Dropout🌟🌟🌟

10 . 我的思考：

03. BP神经网络&BaseLine

1. 什么是深度学习

2. BP神经网络

3. BaseLine

04. Loss Function

1. 类型

2. 正则化

3. 应用场景

05. Tokenization

1. 类型

2.问题

06. Optim