VAE

• 论文链接

1 VAE 的作用 （数据压缩和数据生成）

1.1 数据压缩

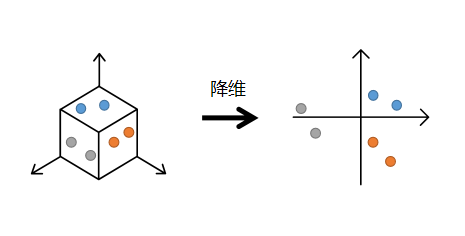
        数据压缩也可以成为数据降维，一般情况下数据的维度都是高维的，比如手写数字（28*28=784维），如果数据维度的输入，机器的处理量将会很大， 而数据经过降维以后，如果保留了原有数据的主要信息，那么我们就可以用降维的数据进行机器学习模型的训练和预测，由于数据量大大缩减，训练和预测的时间效率将大为提高。还有一种好处就是我们可以将数据降维至2D或3D以便于观察分布情况。
        平常最常用到的就是PCA（主成分分析法：将原来的三维空间投影到方差最大且线性无关的两个方向或者说将原矩阵进行单位正交基变换以保留最大的信息量）。

1.2 数据生成

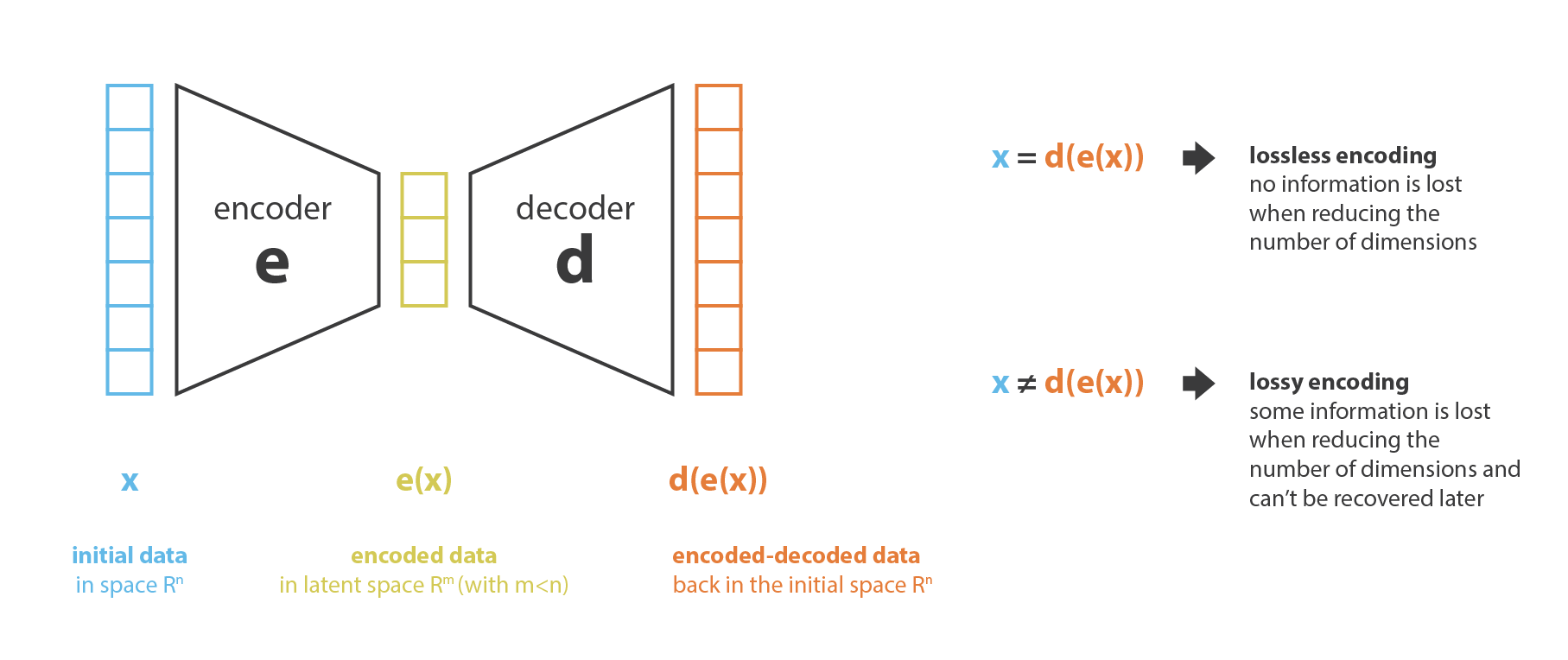
        近年来最火的生成模型莫过于GAN和VAE，这两种模型在实践中体现出极好的性能。
        所谓数据的生成，就是经过样本训练后，人为输入或随机输入数据，得到一个类似于样本的结果。
        比如样本为很多个人脸，生成结果就是一些人脸，但这些人脸是从未出现过的全新的人脸。又或者输入很多的手写数字，得到的结果也是一些手写数字。而给出的数据可能是一个或多个随机数，或者一个分布。然后经过神经网络，将输入的数据进行放大，得到结果。

1.3 数据压缩与数据生成的关系

        在数据生成过程中要输入一些数进去，可是这些数字不能是随随便便的数字吧，至少得有一定的规律性才能让神经网络进行学习(就像要去破译密码，总得知道那些个密码符号表示的含义是什么才可以吧)。
        那如何获得输入数字（或者说密码）的规律呢。这就是数据压缩过程我们所要考虑的问题，我们想要获得数据经过压缩后满足什么规律，在VAE中，我们将这种规律用概率的形式表示。在经过一系列数学研究后：我们最终获得了数据压缩的分布规律，这样我们就可以根据这个规律去抽取样本进行生成，生成的结果一定是类似于样本的数据。

1.4 example

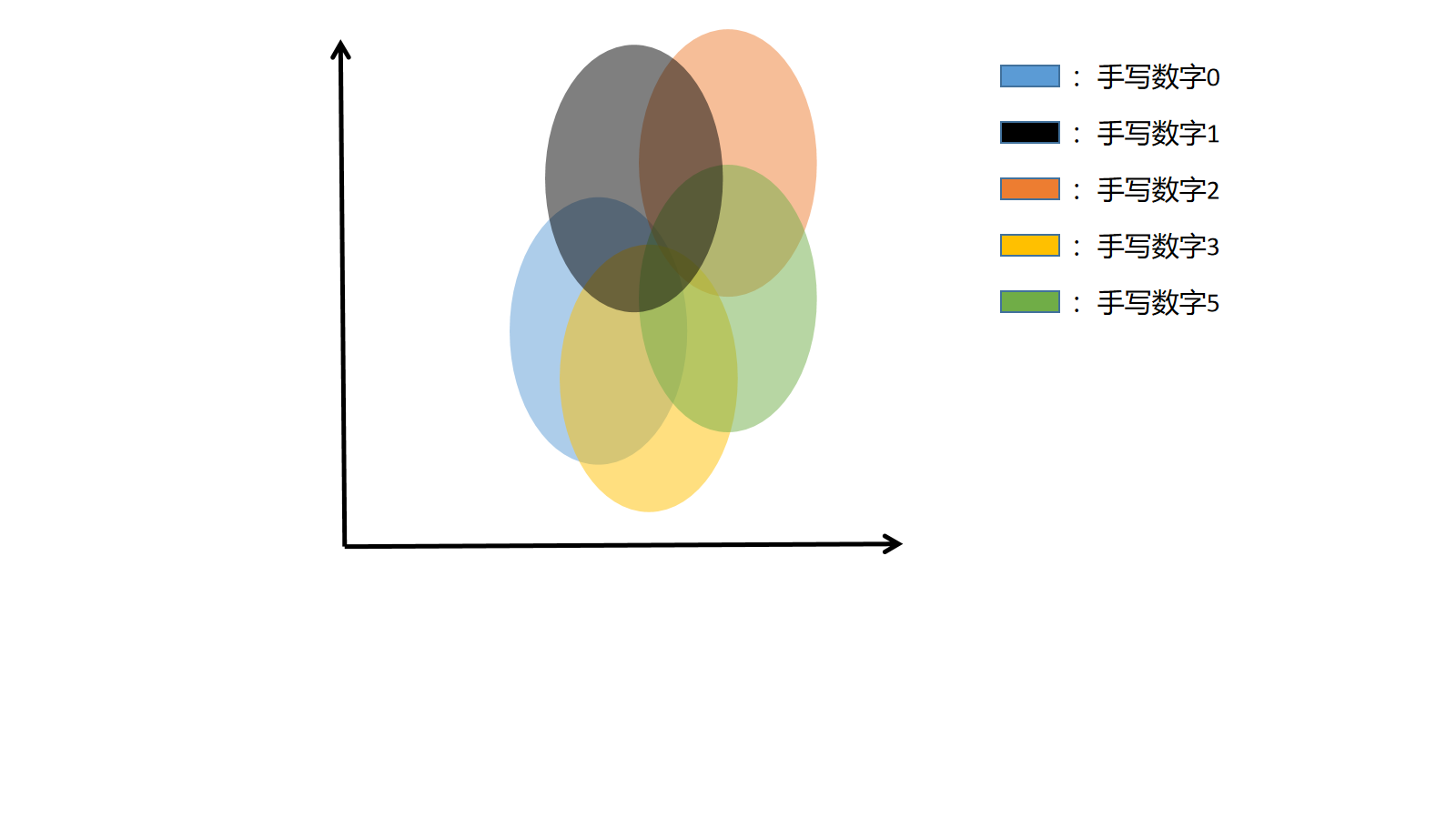
        在前面讲解过，将图片进行某种编码，我们将原来 28*28 = 784 维的图片编码为2维的高斯分布(也可以不是2维，只是为了好可视化), 二维平面的中心就是图片的二维高斯分布的 μ(1) 和 μ(2) ，表示椭圆的中心(注意：这里其实不是椭圆，我们只是把最较大概率的部分框出来)。

        假设一共有5个图片(手写数字0-4)，则在隐空间中一共有5个二维正态分布（椭圆），如果生成过程中在坐标中取的点接近蓝色区域，则说明，最后的生成结果接近数字0，如果在蓝色和黑色交界处，则结果介于0和1之间。

1.5 可能出现的问题

问题：如果每个椭圆离得特别远会发生什么？？？

答案：椭圆之间完全没有交集。

结果：假如随机取数据的时候，取的数据不在任何椭圆里，最后的生成的结果将会非常离谱，根本不知道生成模型生成了什么东西，我们称这种现象为过拟合，因此，我们必须要让这些个椭圆尽可能的推叠在一起，并且尽可能占满整个空间的位置，防止生成不属于任何分类的图片。后面我们会介绍如何将椭圆尽可能堆叠。

        在解决上面问题后，我们就得到了一个较为标准的数据压缩形态，这样我们就可以放心采样进行数据生成。

1.6 VAE 要点总结

        到现在为止，VAE框架已经形成:

• 隐空间(latent space)有规律可循，长的像的图片离得近;
  
• 隐空间随便拿个点解码之后，得到的点有意义;
  
• 隐空间中对应不同标签的点不会离得很远，但也不会离得太近（因为每个高斯的中心部分因为被采样次数多必须特色鲜明，不能跟别的类别的高斯中心离得太近）（VAE做生成任务的基础）;
  
• 隐空间对应相同标签的点离得比较近，但又不会聚成超小的小簇，然而也不会有相聚甚远的情况（VAE做分类任务的基础）;
  

2 理论推导VAE

        怎么去求那么复杂的高斯分布也就是隐空间呢??? 这个问题与变分推断遇到的几乎一样。

2.1 引入变分

        在变分推断中，我们想要通过样本x来估计关于z的分布，也就是后验，用概率的语言描述就是：p(z|x)。根据贝叶斯公式：

$p(z \mid x)=\frac{p(x \mid z) p(z)}{p(x)}$

        p(x)不能直接求, 所以直接贝叶斯这个方法报废，于是我们寻找新的方法. 这时我们想到了变分法,用另一个分布 $Q(z \mid x)$ 来估计 $p(z \mid x, \theta)$ , 变分自编码器的变分就来源于此.
(注释：求泛函极值的方法称为变分法)
(注释2：对于给定的值x∈[x0, x1]，两个可取函数y(x)和y0(x)，函数y(x)在y0(x)处的变分或函数的变分被定义为它们之差，即y(x) - y0(x)。这个变分表示了函数y(x)相对于y0(x)的变化或偏离程度。）

        用一个函数去近似另一个函数，可以看作从概率密度函数所在的函数空间到实数域R的一个函数f，自变量是Q的密度函数，因变量是Q与真实后验密度函数的“距离”，而这一个f关于概率密度函数的“导数”就叫做 变分 ，我们每次降低这个距离，让Q接近真实的后验，就是让概率密度函数朝着“导数“的负方向进行函数空间的梯度下降。所以叫做变分推断。

变分推断和变分自编码器的最终目标是相同的，都是将 $Q(z \mid x)$ 尽量去近似 $p(z \mid x, \theta)$ , 我们知道有一种距离可以量化两种分布的差异Kullback-Leibler divergence—KL散度，我们要尽量减小KL散度。

在这种情况下，我们可以让变分近似后验是一个具有对角协方差结构的多元高斯:

4 参考文献

• vae 导读
• vae 导读2
• vae 参考3